Cos’è la genetica delle popolazioni?
La genetica delle popolazioni si occupa dello studio della costituzione genetica di una popolazione e di come questa cambi, ovvero si evolva, col tempo: di fatto, a partire dall’evoluzione darwiniana e dai principi mendeliani si è via via sviluppata una branca completamente nuova della genetica. Il termine “popolazione” può essere definito in vari modi ma, nel senso più comune, è un’insieme di persone o organismi di una particolare specie vivente in una determinata area geografica. In biologia, una popolazione è la più piccola unità nella quale è possibile il cambiamento evolutivo, perchè permette l’origine di nuovi alleli e il cambiamento della loro frequenza.
Quindi, proprio a partire dalla genetica delle popolazioni, si sono progressivamente sviluppati concetti divenuti poi basilari per la descrizione di questa nuova branca. Ad esempio, si definisce pool genico la somma, in un dato momento, di tutti gli alleli dei membri di una popolazione in grado di riprodursi. In questo modo, è possibile descrivere la variabilità genetica nelle popolazioni in termini di frequenze alleliche e genotipiche.
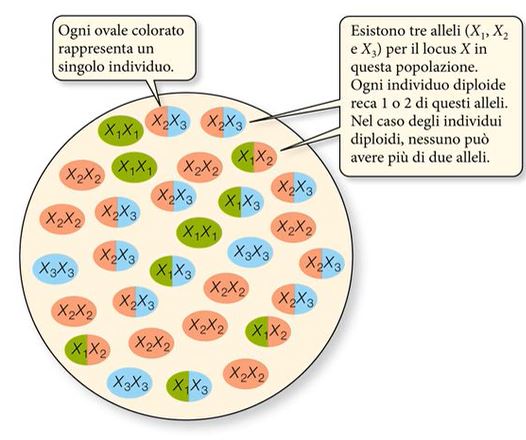
Come emerge dalla Fig.1, il singolo organismo è solo un depositario temporaneo di un piccolo campione del pool genico. Quest’ultimo, inoltre, è stabile solo se le frequenze geniche all’interno di una popolazione non variano, ovvero solo se la popolazione non si sta evolvendo. Nella realtà, le popolazioni sono sempre legate a fenomeni evolutivi e infatti i pool genici sono instabili, cioè caratterizzati da una variazione delle frequenze alleliche. Proprio in merito a queste considerazioni, la genetica delle popolazioni studia la dinamica della variabilità genetica fra individui e popolazioni sotto l’influenza di quattro forze evolutive: selezione naturale, deriva genetica, mutazione e migrazione.
La legge di Hardy-Weinberg
La legge, o equilibrio, di Hardy-Weinberg (indicati spesso con la sigla HW) è un modello della genetica delle popolazioni secondo cui, all’interno di una popolazione ideale, vi è equilibrio delle frequenze alleliche e genotipiche da una generazione all’altra, a meno che non intervengano fattori specifici atti a disturbare l’equilibrio stesso. Il concetto di equilibrio di HW risale al 1908 quando il matematico britannico Godfrey Hardy e il medico tedesco Wilhelm Weinberg dedussero le condizioni necessarie perché la struttura genetica di una popolazione si mantenga invariata nel tempo. Questo è importante poichè fornisce ai biologi uno standard da cui partire per misurare i cambiamenti nella frequenza degli alleli in una popolazione.
Per studiare la variabilità genetica si considera un locus in cui sono presenti due alleli: A e a. Successivamente, si suppone che la frequenza dell’allele dominante A sia espressa come p= f ( A). Allo stesso modo, si indica la frequenza dell’allele recessivo come q= f (a). Da qui è possibile vedere come la frequenza di A e di a devono soddisfare la relazione: p+q=1. Questo è importante, proprio perchè la somma di p e q rappresenta il 100% degli alleli di quel gene. Sulla base delle condizioni idealmente soddisfatte, le frequenze genotipiche manterranno, quindi, i seguenti rapporti:
- Genotipo: AA, Aa, aa
- Fenotipo: p2, 2pq, q2
Poichè le frequenze alleliche determinano le frequenze genotipiche, la distribuzione dei genotipi nella generazioni può essere indicata come:
- p2+2pq+q2=1
Quest’ultima formula altro non è che la legge che Hardy e Weinberg formularono in maniera indipendente.
Possiamo rappresentare il processo della formazione di uno zigote mediante un diagramma di Punnett (Fig. 2):
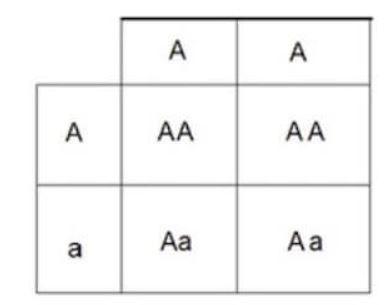
Assunti fondamentali nella legge di Hardy-Weinberg
Nei paragrafi precedenti abbiamo spesso nominato la “popolazione ideale” che è necessaria affinché il modello di HW sia valido. Diamo qui l’elenco completo delle condizioni essenziali all’equilibrio di Hardy-Weinberg:
- Gli accoppiamenti devono essere casuali (popolazione panmittica): in questo modo è come se i geni di tutti gli individui fossero mescolati nel pool genetico ed estratti a sorte per creare i genotipi dei nuovi individui;
- La popolazione deve essere di grandi dimensioni: ciò è richiesto affinché le frequenze siano praticamente coincidenti con le probabilità. Di fatto, più grande è la popolazione, minore è l’effetto delle eventuali fluttuazioni casuali delle frequenze alleliche;
- Non deve esserci flusso genico: in questo modo, senza il verificarsi di immigrazione o emigrazione, il pool genetico è influenzato solo dalle sue dinamiche interne;
- Non devono avvenire mutazioni;
- La selezione naturale non deve influenzare la sopravvivenza di particolari genotipi: in questo contesto, gli individui non differiscono tra loro per il tasso di riproduzione e la capacità riproduttiva.
Equilibrio di Hardy-Weinberg graficato
La legge di Hardy-Weinberg descrive la situazione più semplice di equilibrio genetico di una popolazione. Sebbene sembra difficile ottenere le condizioni dell’equilibrio, esse valgono per molti caratteri in parecchie situazioni; ecco perchè può essere utile rappresentare il tutto in forma di grafico:

É bene notare che il risultato sarà uguale a 1 solo se la popolazione è in equilibrio genetico e che, se diverso da 1, la popolazione sta andando incontro a un fenomeno evolutivo. Inoltre, quando le frequenze alleliche hanno valori medi intorno allo 0.5, la classe più frequente è quella degli eterozigoti (Aa).
Fattori che possono alterare le frequenze alleliche in una popolazione
Già dalla parte introduttiva di questo articolo, è subito emerso come sia difficile che una popolazione in natura soddisfi le condizioni necessarie alla legge di Hardy-Weinberg. Ciò che disturba l’equilibrio è ricollegabile al naturale processo evolutivo che comprende: le mutazioni, la deriva genetica, il flusso genico e la selezione naturale come processi che portano alla modifica della stabilità genetica.
Le mutazioni, ad esempio, cambiano le frequenze alleliche di una popolazione. In particolare, i tassi relativi della mutazione e della reversione determineranno, in assenza di altre forze, le frequenze alleliche di una popolazione. La deriva genetica, invece, è un cambiamento evolutivo sottoposto unicamente alle leggi del calcolo delle probabilità. La frequenza allelica nelle piccole popolazioni non riflette generalmente quella delle grandi popolazioni e con l’avanzare delle generazioni si può avere la prevalenza di alcuni alleli e la scomparsa di altri, indipendentemente dal fatto che ciò sia favorevole per gli individui (effetti a collo di bottiglia e del fondatore).
Per quanto riguarda il flusso genico, questo è un fenomeno che si verifica a causa della migrazione di individui e dello spostamento di gameti da una popolazione a un’altra, introducendo così nuovi alleli nel pool genico. Infine, la selezione naturale proposta da Charles Darwin produce l’adattamento e può essere stabilizzante, direzionale o divergente.
Fonti
- Anthony J.F. Griffiths, Susan R. Wessler, Sean B. Carroll, John Doebley – Genetica, principi di analisi formale; settima edizione; Zanichelli
- Wei Hao and John D. Storey – Extending Tests of Hardy–Weinberg Equilibrium to Structured Populations; Genetics. 2019 Nov; 213(3): 759–770. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC6827367/
- http://ebook.scuola.zanichelli.it/sadavabiologia/l-evoluzione-dopo-darwin-la-teoria-sintetica/document-85
- https://medicinaonline.co/2020/07/08/genetica-di-popolazioni-legge-di-hardy-weinberg-deriva-genetica-migrazione-selezione-naturale/